Python中的数组操作
1、数组变维
函数名称 函数介绍
reshape 在不改变数组元素的条件下,修改数组的形状
flat属性 返回是一个迭代器,可以用 for 循环遍历其中的每一个元素
flatten 以一维数组的形式返回一份数组的副本,对副本的操作不会影响到原数组
ravel 返回一个连续的扁平数组(即展开的一维数组),与 flatten不同,它返回的是数组视图(修改视图会影响原数组)
1.1 reshape
reshape() 函数允许你在不改变数组数据的情况下,改变数组的维度。
reshape() 返回的是一个新的数组,原数组的形状不会被修改。reshape() 可以用于多维数组,例如将一个一维数组重塑为二维数组。
但是,reshape后产生的新数组是原数组的一个视图,即它与原数组共享相同的数据,但可以有不同的形状或维度,且对视图的修改会直接影响原数组。
元素总数必须匹配:新形状中的元素总数必须与原数组中的元素总数相同。
例如,一个长度为6的一维数组可以被重塑为 (2, 3) 或 (3, 2),表示原数组被重塑为2行3列或3行2列的数组,但不能被重塑为 (2, 2)。
#reshape ,改变数组形状
a = np.array([[1, 2, 3], [4, 5, 6]])
b = a.reshape(3, 2)
# print("b=",b)
1.2 flat
import numpy as np
a = np.array([1, 2, 3])
print(a.flat[0])
print(a.flat[1])
print(a.flat[2])
def flat_test():
array_one = np.arange(4).reshape(2,2)
print("原数组元素:")
for i in array_one:
print(i,end=" ")
print()
print("使用flat属性,遍历数组:")
for i in array_one.flat:
print(i,end=" ")
flat_test()
1.3 flatten()
用于将多维数组转换为一维数组。flatten() 返回的是原数组的一个拷贝,因此对返回的数组进行修改不会影响原数组。
语法:ndarray.flatten(order='C')
参数
order: 指定数组的展开顺序。
'C':按行优先顺序展开(默认)。
'F':按列优先顺序展开。
'A':如果原数组是 Fortran 连续的,则按列优先顺序展开;否则按行优先顺序展开。
'K':按元素在内存中的顺序展开。
import numpy as np
# 创建一个二维数组
arr = np.array([[1, 2, 3], [4, 5, 6]])
# 使用 flatten 方法按行优先顺序展开
arrC= arr.flatten(order='C') #按行优先顺序展开
arrF= arr.flatten(order='F') #按列优先顺序展开
arrA= arr.flatten(order='A') #按默认顺序展开
# 输出:
print(arrC)
print(arrF)
print(arrA)
1.4 ravel()
用于将多维数组转换为一维数组。与 flatten() 不同,ravel() 返回的是原数组的一个视图(view),而不是副本。因此,对返回的数组进行修改会影响原数组。
语法:ndarray.ravel()
参数
order: 指定数组的展开顺序。
'C':按行优先顺序展开(默认)。
'F':按列优先顺序展开。
'A':如果原数组是 Fortran 连续的,则按列优先顺序展开;否则按行优先顺序展开。
'K':按元素在内存中的顺序展开。
import numpy as np
# 创建一个二维数组
arr = np.array([[1, 2, 3], [4, 5, 6]])
# 使用 ravel 方法按行优先顺序展开
ravel_arr = arr.ravel()
print(ravel_arr)
# 输出:
# [1 2 3 4 5 6]
ravel_arr[-1] = 7
print(arr)
# 输出:
# [[1 2 3]
# [4 5 7]]
2、数组转置
| 函数名称 | 说明 |
|---|---|
| transpose | 将数组的维度值进行对换,比如二维数组维度(2,4)使用该方法后为(4,2) |
| ndarray.T | 与 transpose 方法相同 |
import numpy as np
def fun1():
arr = np.arange(12).reshape(3, 4)
print("原数组:")
print(arr)
print("使用transpose()函数后的数组:")
print(np.transpose(arr))
def fun2():
arr = np.arange(12).reshape(3, 4)
print("原数组:")
print(arr)
print("数组转置:")
print(arr.T)
fun1()
fun2()
3、升维和降维
多维数组(也称为 ndarray)的维度(或轴)是从外向内编号的。这意味着最外层的维度是轴0,然后是轴1,依此类推。
函数名称 参数 说明
expand_dims(arr, axis) arr:输入数组 axis:新轴插入的位置 在指定位置插入新的轴(相对于结果数组而言),从而扩展数组的维度
squeeze(arr, axis) arr:输入数的组 axis:取值为整数或整数元组,用于指定需要删除的维度所在轴,指定的维度值必须为 1 ,否则将会报错,若为 None,则删除数组维度中所有为 1 的项 删除数组中维度为 1 的项
案例1:增加数组维度
import numpy as np
# 创建一个一维数组
a = np.array([1, 2, 3])
print(a.shape) # 输出: (3,)
# 在第 0 维插入新维度
b = np.expand_dims(a, axis=0)
print(b)
# 输出:
# [[1 2 3]]
print(b.shape) # 输出: (1, 3)
# 在第 1 维插入新维度
c = np.expand_dims(a, axis=1)
print(c)
# 输出:
# [[1]
# [2]
# [3]]
print(c.shape) # 输出: (3, 1)
降维
import numpy as np
# 创建一个数组
c = np.array([[[1, 2, 3]]])
print(c.shape) # 输出: (1, 1, 3)
# 移除第 0 维
d = np.squeeze(c, axis=0)
print(d)
# 输出:
# [[1 2 3]]
print(d.shape) # 输出: (1, 3)
# 移除第 1 维
e = np.squeeze(c, axis=1)
print(e)
# 输出:
# [[1 2 3]]
print(e.shape) # 输出: (1, 3)
# 移除第 2 维
f = np.squeeze(c, axis=2)
print(f)
# 输出:
# ValueError: cannot select an axis to squeeze out which has size not equal to one
print(f.shape)
4 连接数组
函数名称 参数 说明
hstack(tup) tup:可以是元组,列表,或者numpy数组,返回结果为numpy的数组 按水平顺序堆叠序列中数组(列方向)
vstack(tup) tup:可以是元组,列表,或者numpy数组,返回结果为numpy的数组 按垂直方向堆叠序列中数组(行方向)
hstack函数要求堆叠的数组在垂直方向(行)上具有相同的形状。如果行数不一致,hstack() 将无法执行,并会抛出 ValueError 异常。
vstack() 要求堆叠的数组在水平方向(列)上具有相同的形状。如果列数不一致,将无法执行堆叠操作。
vstack() 和 hstack() 要求堆叠的数组在某些维度上具有相同的形状。如果维度不一致,将无法执行堆叠操作。
案例:hstack
import numpy as np
# 创建两个形状不同的数组,行数一致
arr1 = np.array([[1, 2], [3, 4]])
arr2 = np.array([[5], [6]])
print(arr1.shape) # (2, 2)
print(arr2.shape) # (2, 1)
# 使用 hstack 水平堆叠数组
result = np.hstack((arr1, arr2))
print(result)
# 输出:
# [[1 2 5]
# [3 4 6]]
vstack:
import numpy as np
# 创建两个一维数组
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
# 使用 vstack 垂直堆叠数组
result = np.vstack((arr1, arr2))
print(result)
# 输出:
# [[1 2 3]
# [4 5 6]]
5 分割数组
函数名称 参数 说明
hsplit(ary, indices_or_sections) ary:原数组 indices_or_sections:按列分割的索引位置 将一个数组水平分割为多个子数组(按列)
vsplit(ary, indices_or_sections) ary:原数组 indices_or_sections:按行分割的索引位置 将一个数组垂直分割为多个子数组(按行)
import numpy as np
'''
hsplit 函数:
1、将一个数组水平分割为多个子数组(按列)
2、ary:原数组
3、indices_or_sections:按列分割的索引位置
'''
# 创建一个二维数组
arr = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
# 使用 np.hsplit 将数组分割成三个子数组
# 分割点在索引1和3处,这意味着:
# 第一个子数组将包含从第0列到索引1(不包括索引1)的列,即第0列。
# 第二个子数组将包含从索引1(包括索引1)到索引3(不包括索引3)的列,即第1列到第2列。
# 第三个子数组将包含从索引3(包括索引3)到末尾的列,即第3列。
result = np.hsplit(arr, [1, 3])
# 查看结果
print("第一个子数组:\n", result[0]) # 输出包含第0列的子数组
print("第二个子数组:\n", result[1]) # 输出包含第1列和第2列的子数组
print("第三个子数组:\n", result[2]) # 输出包含第3列的子数组
'''
vsplit 函数:
1、将一个数组垂直分割为多个子数组(按行)
2、ary:原数组
3、indices_or_sections:按列分割的索引位置
'''
array_one = np.arange(12).reshape(2,6)
print('array_one 原数组:\n', array_one)
array_two = np.vsplit(array_one,[1])
print('vsplit 之后的数组:\n', array_two)
6 、矩阵运算
np.dot
是一个通用的点积函数,适用于多种维度的数组。
对于二维数组(矩阵),np.dot 等价于矩阵乘法。
对于一维数组(向量),np.dot 计算的是向量的点积(内积)。
案例1:矩阵运算
import numpy as np
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
result = np.dot(a, b)
print(result)
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
result = np.dot(a, b)
print(result)
np.matmul
是专门用于矩阵乘法的函数,适用于二维及更高维度的数组。
案例:矩阵相乘
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
result = np.matmul(a, b)
print(result)
np.linalg.det
a = np.array([[1, 2], [3, 4]],dtype=int)
# 计算行列式
det_a = np.linalg.det(a)
print(det_a)
#输出:
-2.0000000000000004
结果不是-2,这是由于浮点数的二进制表示和计算过程中的舍入误差导致的。可以通过四舍五入来近似表示:
det_a = np.round(np.linalg.det(a))
7、数组元素的增删改查
7.1 resize
| 函数名称 | 参数 | 说明 |
|---|---|---|
| resize(a, new_shape) | a:操作的数组 new_shape:返回的数组的形状,如果元素数量不够,重复数组元素来填充新的形状 | 返回指定形状的新数组 |
import numpy as np
array_one = np.arange(6).reshape(2, 3)
print(array_one)
print('resize 后数组:\n', np.resize(array_one, (3, 4)))
# 输出:
# [[0 1 2 3]
# [4 5 0 1]
# [2 3 4 5]]
最后一行代码将数组形状修改为(3, 4),原数组的元素数量不够,则重复原数组的元素填充。
7.2 append
函数名称 参数 说明
append(arr, values, axis=None) arr:输入的数组 values:向 arr 数组中添加的值,需要和 arr 数组的形状保持一致 axis:默认为 None,返回的是一维数组;当 axis =0 时,追加的值会被添加到行,而列数保持不变,若 axis=1 则与其恰好相反 在数组的末尾添加值,返回一个一维数组
案例:
'''
append(arr, values, axis=None) 函数:
1、将元素值添加到数组的末尾,返回一个一维数组
2、arr:输入的数组
3、values:向 arr 数组中添加的值,需要和 arr 数组的形状保持一致
4、axis:默认为 None,返回的是一维数组;当 axis =0 时,追加的值会被添加到行,而列数保持不变,若 axis=1 则与其恰好相反
'''
def append_test():
array_one = np.arange(6).reshape(2,3)
print('原数组:\n', array_one)
array_two = np.append(array_one,[[1,1,1],[1,1,1]],axis=None)
print('append 后数组 axis=None:\n', array_two)
array_three = np.append(array_one, [[1, 1, 1], [1, 1, 1]], axis=0)
print('append 后数组 axis=0:\n', array_three)
array_three = np.append(array_one, [[1, 1, 1], [1, 1, 1]], axis=1)
print('append 后数组 axis=1:\n', array_three)
7.3 insert
函数名称 参数 说明
insert(arr, obj, values, axis) arr:输入的数组 obj:表示索引值,在该索引值之前插入 values 值 values:要插入的值 axis:默认为 None,返回的是一维数组;当 axis =0 时,追加的值会被添加到行,而列数保持不变,若 axis=1 则与其恰好相反 沿规定的轴将元素值插入到指定的元素前
案例:
import numpy as np
def insert_test():
array_one = np.arange(6).reshape(2,3)
print('原数组:\n', array_one)
array_two = np.insert(array_one, 1, [6],axis=None)
print('insert 后数组 axis=None:\n', array_two)
# 在索引为1的行插入[6],并自动广播
array_three = np.insert(array_one,1, [6], axis=0)
print('insert 后数组 axis=0:\n', array_three)
# 在索引为1的列插入[6],并自动广播
array_three = np.insert(array_one, 1, [6], axis=1)
print('insert 后数组 axis=1:\n', array_three)
array_three = np.insert(array_one, 1, [6,7], axis=1)
print('insert 后数组 axis=1:\n', array_three)
# 在列上插入数组的形状和原数组列的形状不一致
# ValueError: could not broadcast input array from shape (3,1) into shape (2,1)
array_three = np.insert(array_one, 1, [6,7,8], axis=1)
print('insert 后数组 axis=1:\n', array_three)
如果obj为-1,表示插入在倒数第一个元素之前,不是在最后一列。
array_three = np.insert(array_one, -1, [6,7], axis=1)
print('insert 后数组 axis=1:\n', array_three)
#输出:
[[0 1 6 2]
[3 4 7 5]]
7.4 delete
函数名称 参数 说明
delete(arr, obj, axis) arr:输入的数组 obj:表示索引值,要删除数据的索引 axis:默认为 None,返回的是一维数组;当 axis =0 时,删除指定的行,若 axis=1 则与其恰好相反 删掉某个轴上的子数组,并返回删除后的新数组
案例:
一维数组:
import numpy as np
# 创建一个 NumPy 数组
arr = np.array([1, 2, 3, 4, 5, 6])
# 删除索引为 2 和 4 的元素
new_arr = np.delete(arr, [2, 4])
print(new_arr)
二维数组:
import numpy as np
def delete_test():
array_one = np.arange(6).reshape(2,3)
print('原数组:\n', array_one)
array_two = np.delete(array_one,1,axis=None)
print('delete 后数组 axis=None:\n', array_two)
array_three = np.delete(array_one,1, axis=0)
print('delete 后数组 axis=0:\n', array_three)
array_three = np.delete(array_one, 1, axis=1)
print('delete 后数组 axis=1:\n', array_three)
7.5 argwhere
import numpy as np
'''
argwhere(a) 函数:
1、返回数组中非 0 元素的索引,若是多维数组则返回行、列索引组成的索引坐标
'''
def argwhere_test():
array_one = np.arange(6).reshape(2,3)
print('原数组:\n', array_one)
print('argwhere 返回非0元素索引:\n', np.argwhere(array_one))
print('argwhere 返回所有大于 1 的元素索引:\n', np.argwhere(array_one > 1))
7.6 unique
函数名称 参数 说明
unique(ar, return_index=False, return_inverse=False, return_counts=False, axis=None) ar:输入的数组 return_index:如果为 True,则返回新数组元素在原数组中的位置(索引) return_inverse:如果为 True,则返回原数组元素在新数组中的位置(逆索引) return_counts:如果为 True,则返回去重后的数组元素在原数组中出现的次数 删掉某个轴上的子数组,并返回删除后的新数组
案例1:返回唯一元素的索引
import numpy as np
# 创建一个 NumPy 数组
arr = np.array([1, 2, 2, 3, 4, 4, 5])
unique_elements, indices = np.unique(arr, return_index=True)
print(unique_elements)
print(indices)
8、统计函数
8.1 amin() 和 amax()
计算数组沿指定轴的最小值与最大值,并以数组形式返回
对于二维数组来说,axis=1 表示沿着水平方向,axis=0 表示沿着垂直方向
'''
numpy.amin() 和 numpy.amax() 函数:
1、计算数组沿指定轴的最小值与最大值,并以数组形式返回
2、对于二维数组来说,axis=1 表示沿着水平方向,axis=0 表示沿着垂直方向
'''
def amin_amax_test():
array_one = np.array([[1,23,4,5,6],[1,2,333,4,5]])
print('原数组元素:\n', array_one)
print('原数组水平方向最小值:\n', np.amin(array_one, axis=1))
print('原数组水平方向最大值:\n', np.amax(array_one, axis=1))
print('原数组垂直方向最小值:\n', np.amin(array_one, axis=0))
print('原数组垂直方向最大值:\n', np.amax(array_one, axis=0))
8.2 ptp()
计算数组元素中最值之差值,即最大值 - 最小值
对于二维数组来说,axis=1 表示沿着水平方向,axis=0 表示沿着垂直方向
# 创建一个二维数组
arr = np.array([[1, 2, 3], [4, 5, 6]])
# 使用 np.ptp 计算峰峰值
ptp_value = np.ptp(arr)
print(ptp_value)
# 输出:
# 5
# 使用 np.ptp 按行计算峰峰值
ptp_values_row = np.ptp(arr, axis=1)
# 使用 np.ptp 按列计算峰峰值
ptp_values_col = np.ptp(arr, axis=0)
print(ptp_values_row)
# 输出:
# [2 2]
print(ptp_values_col)
# 输出:
# [3 3 3]
8.3 median()
# 创建一个二维数组
arr = np.array([[1, 2, 3], [4, 5, 6]])
# 使用 np.median 计算中位数
median_value = np.median(arr,axis=None)
print(median_value)
# 输出:
# 3.5
# 使用 np.median 按行计算中位数
median_values_row = np.median(arr, axis=1)
# 使用 np.median 按列计算中位数
median_values_col = np.median(arr, axis=0)
print(median_values_row)
# 输出:
# [2. 5.]
print(median_values_col)
# 输出:
# [2.5 3.5 4.5]
8.4 mean()
# 创建一个一维数组
arr = np.array([1, 2, 3, 4, 5])
# 使用 np.mean 计算平均值
mean_value = np.mean(arr)
print(mean_value)
# 输出:
# 3.0
# 创建一个二维数组
arr = np.array([[1, 2, 3], [4, 5, 6]])
# 使用 np.mean 计算平均值
mean_value = np.mean(arr)
print(mean_value)
# 输出:
# 3.5
# 使用 np.mean 按行计算平均值
mean_values_row = np.mean(arr, axis=1)
# 使用 np.mean 按列计算平均值
mean_values_col = np.mean(arr, axis=0)
print(mean_values_row)
# 输出:
# [2. 5.]
print(mean_values_col)
# 输出:
# [2.5 3.5 4.5]
8.5 average()
加权平均值是将数组中各数值乘以相应的权数,然后再对权重值求总和,最后以权重的总和除以总的单位数(即因子个数);根据在数组中给出的权重,计算数组元素的加权平均值。该函数可以接受一个轴参数 axis,如果未指定,则数组被展开为一维数组。
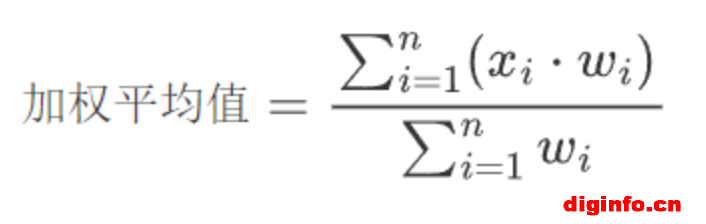
其中 xi是数组中的元素,wi是对应的权重。
如果所有元素的权重之和等于1,则表示为数学中的期望值。
# 创建一个一维数组
arr = np.array([1, 2, 3, 4, 5])
# 创建权重数组
weights = np.array([0.1, 0.2, 0.3, 0.2, 0.2])
# 使用 np.average 计算加权平均值
average_value = np.average(arr, weights=weights)
print(average_value)
# 输出:
# 3.2
8.6 var()
在 NumPy 中,计算方差时使用的是统计学中的方差公式,而不是概率论中的方差公式,主要是因为 NumPy 的设计目标是处理实际数据集,而不是概率分布。
np.var 函数默认计算的是总体方差(Population Variance),而不是样本方差(Sample Variance)。
总体方差:
对于一个总体数据集 X={x1,x2,…,xN},总体方差的计算公式为:
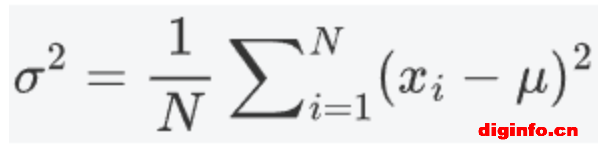
其中:
N是总体数据点的总数。
μ是总体的均值。
# 创建一个数组
arr = np.array([1, 2, 3, 4, 5])
# 计算方差
variance = np.var(arr)
print(variance)
#输出:2
n是样本数据点的总数。
xˉ是样本的均值。
# 创建一个数组
arr = np.array([1, 2, 3, 4, 5])
# 计算方差
variance = np.var(arr, ddof=1)
print(variance)
#输出:2.5
8.7 std()
# 创建一个数组
arr = np.array([1, 2, 3, 4, 5])
# 计算标准差
std_dev = np.std(arr)
print(std_dev)
# 输出:1.4142135623730951

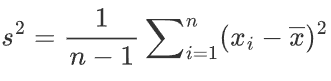
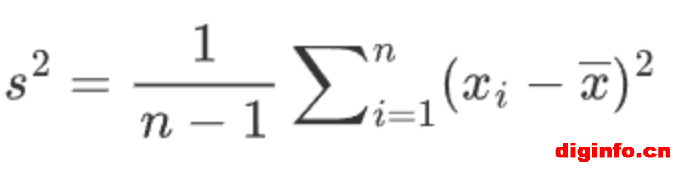

全部评论